うちーノート

少しでも数学好きが増えますようにというブログ

f(x)=sinx/x について考えよう【sinc関数】

解析学 高校数学

 

はじめに 

全記事をまとめてあります．

ぜひ下のリンクから確認してください．

uchii-memo.hatenablog.com

 

この記事の目的：\displaystyle f(x)=\frac{\sin x}{x} について考える．

 

sinc関数

f(x)=\displaystyle \frac{\sin x}{x}

上記の関数を「sinc（シンク）関数」と呼ぶ．

 

以下、順に性質等を確認していこう．

 

極限

課題：\displaystyle \lim_{x\rightarrow 0} \frac{\sin x}{x} を考える 

 

解法①：「はさみこみ」による解法

３つの図形の大小関係を比較する．

f:id:uchii-room:20190630141138p:plain

まずは上図のような三角形を考える．

高さが\sin x のため，この三角形の面積S_1 は以下のように表せる．

\displaystyle S_1=\frac{\sin x}{2}

f:id:uchii-room:20190630141141p:plain

次に，上図のような扇型を考える．

この扇型の面積S_2は以下のように表される．

\displaystyle S_2=\pi\frac{x}{2\pi}=\frac{x}{2}

f:id:uchii-room:20190630141150p:plain

最後に，上手のような直角三角形を考える．

高さが\tan x で表されるため，この直角三角形の面積S_3は以下のようになる．

\displaystyle S_3=\frac{\tan x}{2}

 

３つの図形を重ね合わせてみる．

f:id:uchii-room:20190630141405p:plain

図形の面積を比較すると以下がいえる．（S_1=ピンク，S_2=紫，S_3=青）

S_1\lt S_2\lt S_3

\displaystyle \frac{\sin x}{2}\lt\frac{x}{2}\lt\frac{\tan x}{2}

上式を変形すると，

\displaystyle \sin x\lt x\lt\frac{\sin x}{\cos x}

\displaystyle 1\lt\frac{x}{\sin x}\lt\frac{1}{\cos x}

\displaystyle 1\gt\frac{\sin x}{x}\gt\cos x

各々で極限をとると，

\displaystyle \lim_{x\rightarrow 0}1\gt\lim_{x\rightarrow 0}\frac{\sin x}{x}\gt\lim_{x\rightarrow 0}\cos x

\displaystyle 1\gt\lim_{x\rightarrow 0}\frac{\sin x}{x}\gt 1

はさみこみの原理より以下がいえる．

\displaystyle \lim_{x\rightarrow 0}\frac{\sin x}{x}=1

 

解法② ：「ロピタルの定理」を用いた解法

ロピタルの定理

 

\displaystyle\lim_{x\rightarrow a} \frac{f(x)}{g(x)}=\lim_{x\rightarrow a} \frac{f'(x)}{g'(x)}

 

満たすべき条件

1. 関数f(x),g(x) がx=aを含む区間Iで連続である．

2. 区間Iのx\neq aで微分可能かつg'(x)\neq 0．

3. 不定形である．

4. \displaystyle\lim_{x\rightarrow a} \frac{f'(x)}{g'(x)} が存在する．

 

条件の確認

f(x)=\sin x, g(x)=xより，条件1,2,4は自明．

\displaystyle \lim_{x\rightarrow 0} \sin x=0，\displaystyle \lim_{x\rightarrow 0} x=0

よって不定形であるため，条件3も満たされる．

不定形とは，\displaystyle \frac{f(x)}{g(x)} において，以下のどちらかのパターンをとるもの．

 

1. \displaystyle\lim_{x\rightarrow a} f(x)=0 \land \lim_{x\rightarrow a} g(x)=0

 

2. \displaystyle\lim_{x\rightarrow a} f(x)=\infty \land \lim_{x\rightarrow a} g(x)=\infty

 

  

ロピタルの定理より，

\displaystyle \lim_{x\rightarrow 0} \frac{\sin x}{x}=\lim_{x\rightarrow 0} \frac{\cos x}{1}=1

 

sinc関数のグラフ

\displaystyle f(x)=\frac{\sin x}{x} をグラフ化した．

f:id:uchii-room:20190630150127p:plain

f:id:uchii-room:20190630150141p:plain

\displaystyle g(x)=\frac{1}{x} に沿うことがわかる．

また\displaystyle \lim_{x\rightarrow 0} \frac{\sin x}{x}=1 であることも可視化できる．

 

sinc関数の微分

課題：\displaystyle \frac{d}{dx}sinc(x) を考える．

 

積の微分法

\displaystyle \frac{d}{dx}\{f(x)g(x)\}=f'(x)g(x)+f(x)g'(x)

 

積の微分法を用いる．

\displaystyle \left(\frac{\sin x}{x}\right) '=\left(\frac{1}{x}\right) '\sin x+\frac{1}{x}(\sin x)'=-\frac{\sin x}{x^2}+\frac{\cos x}{x}

 

 

sinc関数の積分

課題：\displaystyle \int_0^\infty \frac{\sin x}{x} dx を考える．

 

長いので別記事に分けました．下のリンクからどうぞ．

 記事：sinc関数の積分の解法

 

結果：\displaystyle \int_0^\infty \frac{\sin x}{x}dx=\frac{\pi}{2}

 

sinc関数の２乗の積分

課題：\displaystyle \int_0^\infty \frac{\sin^2 x}{x^2} dx を考える．

 

条件：\displaystyle \int_0^\infty \frac{\sin x}{x}dx=\frac{\pi}{2} は既知として使用して良いことにする．

 

解法

部分積分により\displaystyle \frac{1}{x^2}部分の次数を下げて\displaystyle \int_0^\infty \frac{\sin x}{x}dx=\frac{\pi}{2} が使える状態に誘導する．

計算

\displaystyle \int_0^\infty \frac{\sin^2 x}{x^2} dx

部分積分より，

　\displaystyle =\left[-\frac{1}{x}\sin^2 x\right]_0^\infty+\int_0^\infty \frac{2\sin x\cos x}{x} dx

　\displaystyle =\int_0^\infty \frac{\sin 2x}{x} dx

2x=t に置換する．

　\displaystyle =\int_0^\infty \frac{\sin t}{\frac{t}{2}} \frac{1}{2}dt

　\displaystyle =\int_0^\infty \frac{\sin t}{t} dt 

　\displaystyle =\frac{\pi}{2}

 

\displaystyle \therefore \int_0^\infty \frac{\sin^2 x}{x^2} dx=\frac{\pi}{2}

 

sinc関数の積分について 

sinc関数の広義積分

\displaystyle  \int_0^\infty \frac{\sin x}{x}dx=\frac{\pi}{2}

sinc関数の２乗の広義積分

\displaystyle  \int_0^\infty \frac{\sin^2 x}{x^2} dx=\frac{\pi}{2}

両者同じ結果が得られた．

\displaystyle  \int_0^\infty \frac{\sin x}{x}dx=\int_0^\infty \frac{\sin^2 x}{x^2} dx=\frac{\pi}{2}

このことについてグラフを見ながら考えていく．

 

各々のグラフ

\displaystyle  \int_0^\infty \frac{\sin x}{x}dx

f:id:uchii-room:20190701222601p:plain

\displaystyle  \int_0^\infty \frac{\sin^2 x}{x^2} dx

f:id:uchii-room:20190701223339p:plain

 

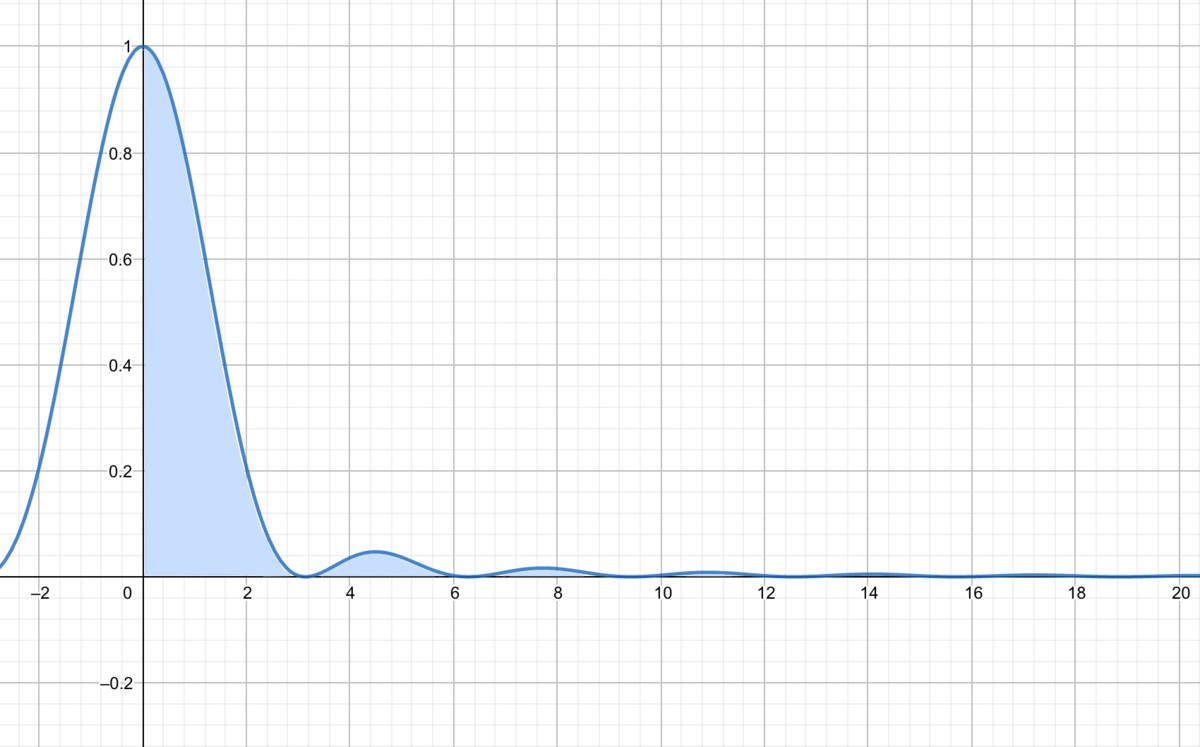
グラフの比較

f:id:uchii-room:20190701223454p:plain

\displaystyle  \int_0^\infty \frac{\sin x}{x}dx

・１つ１つの面積は大きいが，x軸より下にできる面積は負としてカウントされる. 

＝面積の損が大きい

 

\displaystyle  \int_0^\infty \frac{\sin^2 x}{x^2} dx

→１つ１つの面積は小さいがすべて正としてカウントされている. 

＝面積の損が全くない

 

このことから、以下の結果が得られたことがイメージできる．

\displaystyle  \int_0^\infty \frac{\sin x}{x}dx=\int_0^\infty \frac{\sin^2 x}{x^2} dx=\frac{\pi}{2}

 

まとめ

 \displaystyle f(x)=\frac{\sin x}{x} について

 

・\displaystyle \lim_{x\rightarrow0} f(x)=1

・\displaystyle f'(x)=-\frac{\sin x}{x^2}+\frac{\cos x}{x}

・\displaystyle  \int_0^\infty f(x) dx=\int_0^\infty {f(x)}^2 dx=\frac{\pi}{2}

 

・y=f(x)

f:id:uchii-room:20190630150127p:plain

 

最後に

全記事をまとめてあります．

ぜひ下のリンクから確認してください．

uchii-memo.hatenablog.com