うちーノート

少しでも数学好きが増えますようにというブログ

【球体の表面積】中学生に分かるように真剣に考えてみた

中学数学 幾何学

 

はじめに

全記事をまとめてあります．

ぜひ下のリンクから確認してください．

uchii-memo.hatenablog.com

 

この記事の目的：球体の表面積を求める式の意味を中学生にも分かるように説明する．

 

球の表面積

f:id:uchii-room:20190406115817p:plain

球の表面積S=4\pi r^2

目的：上式になる理由を説明する．

 

説明は４種類考えました．

 

前提の知識

円周=2\pi r 

周の長さなどは以下の通り

f:id:uchii-room:20190108232451p:plain 

方法①：球の表面のマクを外す

指針（考え方）

球体の表面に薄いマクが張っていることをイメージする。

薄いマクの面積＝表面積

 

f:id:uchii-room:20190106232736p:plain

指針：マクをはがして平面にする→面積を計算する\fallingdotseq表面積

 

はがし方①

下図のように切り込みを入れてはがす。

 

f:id:uchii-room:20190107001609p:plain 

 

f:id:uchii-room:20190107003154p:plain

横の長さ＝球の一周分の長さ=2\pi r

縦の長さ＝球の半周分の長さ=\pi r

形を単純にしてだいたいの面積を求める．

 

f:id:uchii-room:20190107004402p:plain

面積＝\pi r\times2\pi r\times\frac{1}{2}=\pi^2 r^2

　　＝3.14\pi r^2

 

形を切り落として考えているため，実際の面積はもう少し大きいと考えられる． 

球体の表面積S > 3.14\pi r^2 …(1)

 

はがし方②

次のように切り込みを入れてはがしてみる．（点の部分はくっつけたままにしておく）

f:id:uchii-room:20190108002629p:plain

 

f:id:uchii-room:20190108005345p:plain

円のように見えないこともないので，この図形を円と捉えることにする．

円の半径＝球の周の長さの\displaystyle\frac{1}{4} ＝\displaystyle\frac{1}{2}\pi r

半径\displaystyle \frac{1}{2}\pi r の円と見立てて面積を求めると，

面積＝\displaystyle\frac{1}{2}\pi r\times\frac{1}{2}\pi r\times\pi=\frac{\pi^2}{4}\pi r^2

これが半球分なので２倍する．

\displaystyle\frac{\pi^2}{4}\pi r^2\times 2=\frac{\pi^2}{2}\pi r^2=4.93\pi r^2

 

形を大きく見積もって計算しているため，実際の面積はもう少し小さいと考えられる． 

球の表面積S < 4.93 \pi r^2 …(2)

 

２つの比較

(1)(2)より，

3.14\pi r^2 < 球の表面積S < 4.93\pi r^2

 

方法②：輪切りにする

指針（考え方）

f:id:uchii-room:20190107010433p:plain

この円柱の側面積＝2r\times2\pi r=4\pi r^2

球の表面積の公式と同じ式をしていることが分かる．

 

あなたは今、球の表面積を求める公式を知らないものとします．

円柱の側面積＝球の表面積 を示すことによって，

（円柱の側面積＝4\pi r^2 なので，）

球体の表面積＝4\pi r^2 を示すことができます．

 

 

輪切りの考え方

円柱と球を真横に並べる．

f:id:uchii-room:20190107012346p:plain

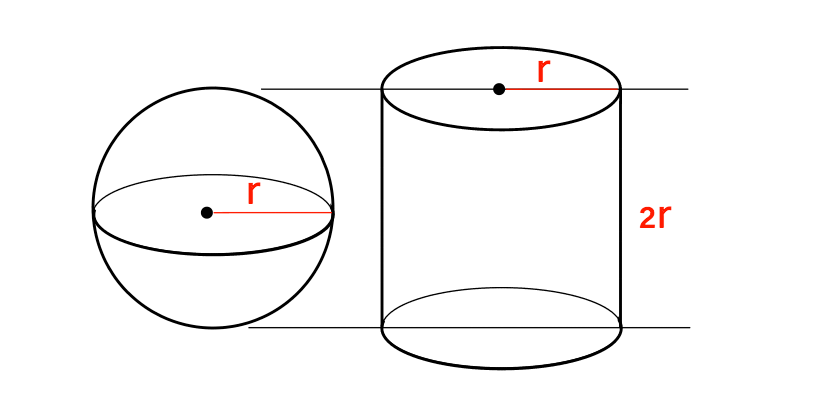
自分の好きな高さで輪切りにする．

f:id:uchii-room:20190107013456p:plain 

輪切りされた部分の表面積（赤色）が等しいことを確かめる．

 

どの位置で輪切りにしても面積が等しい＝表面積が等しい，といえる．

 

思考実験 

①球のちょうど真ん中で輪切りにする．

f:id:uchii-room:20190109221602p:plain

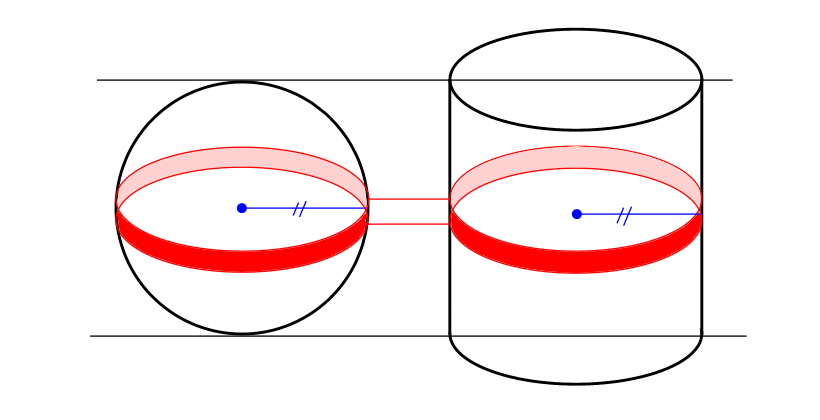
２つとも半径（青色）が同じ→面積も同じ．

 

②真ん中より少し上で輪切りにする．

f:id:uchii-room:20190109222359p:plain

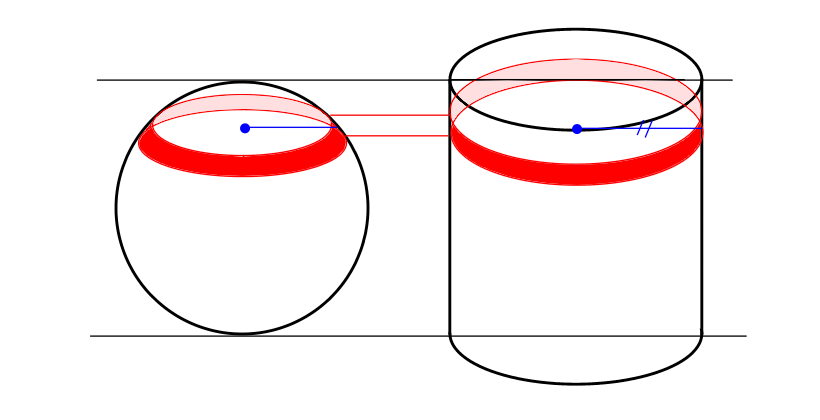
球体のほうの半径が小さくなった．

→面積も小さくなったのではないか？

 

（横から見た図）

f:id:uchii-room:20190107015545p:plain

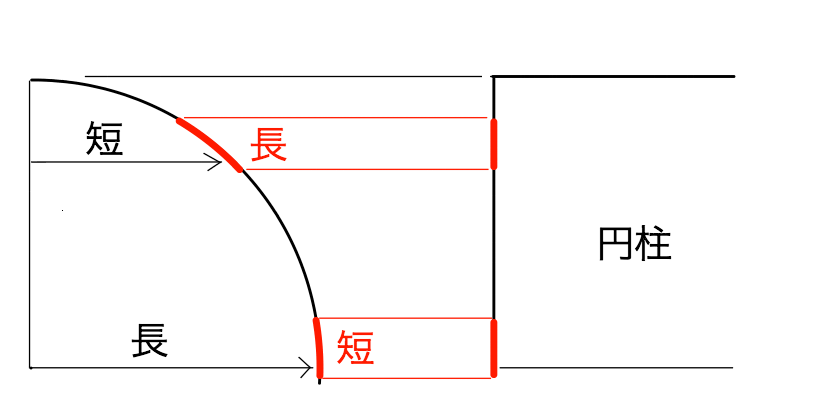
半径は短くなったが、接する部分（赤色）が長くなっている．

→面積は等しいとイメージできる．

 

どこで切っても面積は変わらない、と考えられる.

輪切りの考え方から，球体の表面積＝円柱の側面積

 

\therefore 球体の表面積＝円柱の側面積＝4\pi r^2 

 

方法③：球体を細かく切る

指針（考え方）

球体を切って細かくする→表面積を考える

 

細かく切る

球体の表面に薄いマクがはってあることをイメージする.

マクの面積＝球の表面積

f:id:uchii-room:20190106232736p:plain

球体を図のように切る．

f:id:uchii-room:20190109154838p:plain

これを6回繰り返す．

f:id:uchii-room:20190109171329p:plain

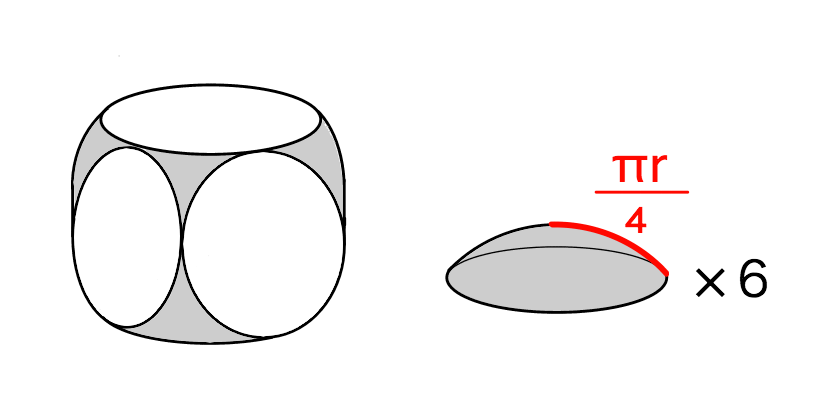
立方体のような物体1つと，UFO型の物体が6つできた．

（灰色の部分＝球の表面積だった部分）

 

UFO型の物体

UFO型の灰色部分の面積はいくつか．

f:id:uchii-room:20200113225912p:plain

灰色の部分を半径\displaystyle\frac{\pi r}{4} の円とみなすと，

面積＝\displaystyle \frac{\pi r}{4}\times \frac{\pi r}{4} \times \pi=\frac{\pi^2}{16}\pi r^2

この物体が6つあるので，

\displaystyle \frac{\pi^2}{16}\pi r^2 \times 6=\frac{3\pi^2}{8}\pi r^2=3.70\pi r^2

 

立方体のような立体

立方体のような物体に付いている灰色部分の面積はいくらか．

この物体を一辺が\sqrt{2}r の立方体に入れる．

f:id:uchii-room:20190109174406p:plain

f:id:uchii-room:20190109182620p:plain

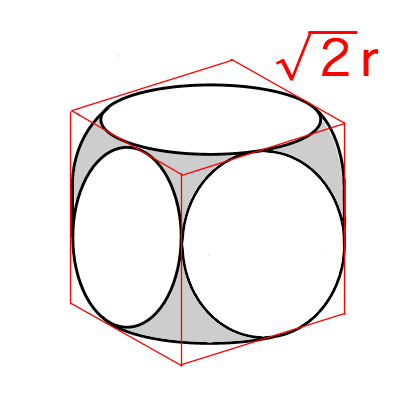
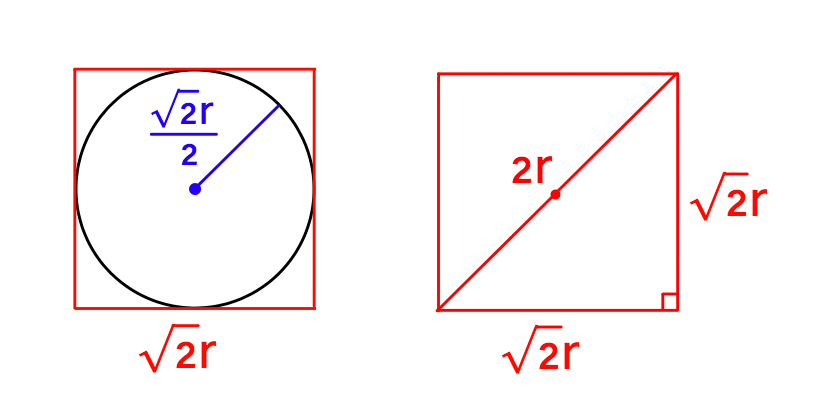
円の半径＝立方体の一辺の半分＝\displaystyle\frac{\sqrt{2}}{2}r（左図）

斜めの線＝2r （三平方の定理）（右図）

f:id:uchii-room:20190109182504p:plain

上図の① \displaystyle =r-\frac{\sqrt{2}}{2}r

②=①\times 2\displaystyle =\left(r-\frac{\sqrt{2}}{2}r\right)\times 2=2r-\sqrt{2}r

f:id:uchii-room:20190109183835p:plain

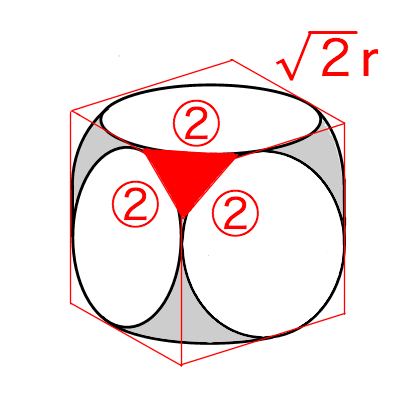
②の線＝赤い三角形の一辺を表す．

灰色部分の面積を赤い正三角形とみなして面積を計算する．

 

赤い三角形の一辺＝2r-\sqrt{2}r=\left(2-\sqrt{2}\right)r

f:id:uchii-room:20190109184637p:plain

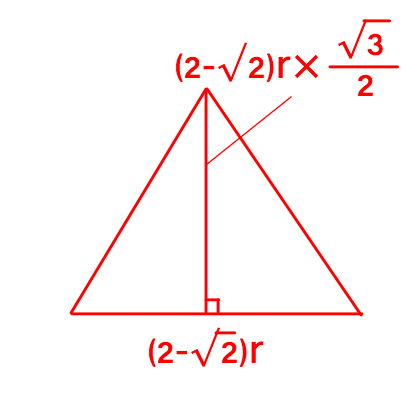
面積=\displaystyle \left(2-\sqrt{2}\right)r\times\frac{\sqrt{3}}{2}\times\left(2-\sqrt{2}\right)r\times\frac{1}{2}=\frac{\sqrt{3}}{2}\left(3-2\sqrt{2}\right)r^2

同じ三角形が８つ考えられる．（灰色の部分が８箇所ある）

\displaystyle \frac{\sqrt{3}}{2}\left(3-2\sqrt{2}\right)r^2\times 8=\frac{8\sqrt{3}}{2}\left(3-2\sqrt{2}\right)r^2

少し変形して，

\displaystyle \frac{8\sqrt{3}}{2\pi}\left(3-2\sqrt{2}\right)\pi r^2=0.38\pi r^2

 

結論

UFO型の物体に付いていた灰色部分の面積＝3.70\pi r^2

立方体のような物体に付いていた面積＝0.38\pi r^2

 

球の表面積＝3.70\pi r^2+0.38\pi r^2=4.08\pi r^2 

 

説明④：パップスギュルダンの定理を使う

 

球面を図のように切り分ける．

f:id:uchii-room:20190109201059p:plain

切って広げる．

f:id:uchii-room:20190109201715p:plain

この帯の台形なので，面積は以下のように求められる．

面積 \displaystyle s=(A+B)\times L\times \frac{1}{2}=\frac{A+B}{2}L

f:id:uchii-room:20190109202303p:plain

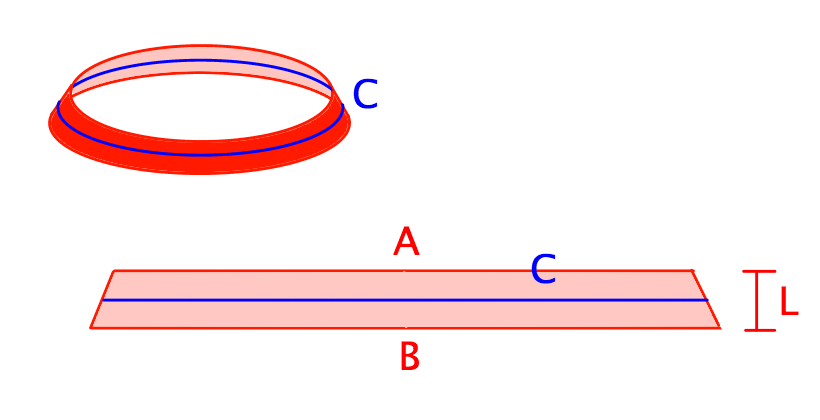
上図より，面積 sの式は以下のように表せる．

面積 \displaystyle s=\frac{A+B}{2}L=CL…(1)

 

回転体と考える

f:id:uchii-room:20190109203435p:plain

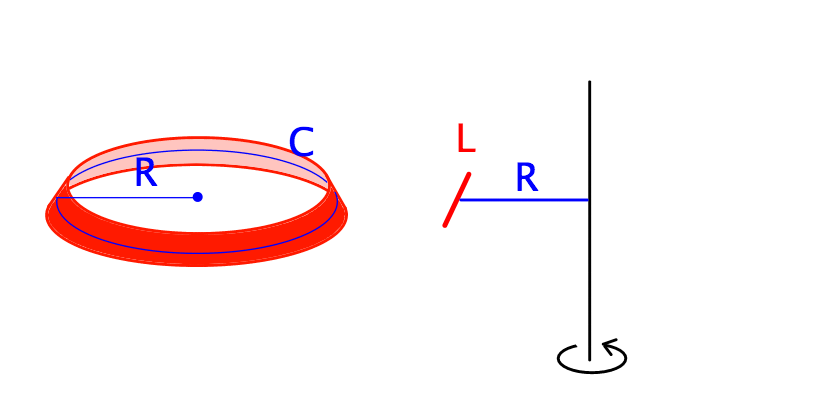
左図の図形は，右図を回転させるとできる．

このときC=2\pi R である．よって，(1)式は以下のように変形できる．

 \displaystyle s=CL=2\pi RL…(2)

 

面積を知るには，RL の値がわかれば良さそう．

 

RLとは

（先述の右図）

f:id:uchii-room:20190109205124p:plain

先述の右図について，LとRを分けて２つ表示してみた．

ピンクの三角形と水色の三角形は相似であると分かる．

よって以下の比例式が成立する．

L : ②=① : R  

したがって，

RL= ①\times ②…(3)

 

①と②の長さが分かれば良さそう．

 

①②とは

①と②はどの部分の長さを表すかを考える．

f:id:uchii-room:20190109210556p:plain

上図より，②は球体の半径を表すことは明らかである．

②=r …(4)

 

あとは①の正体がわかればいい．

f:id:uchii-room:20190109211757p:plain

上図より，①を全て足すと球の直径になることが分かる．

①の総和=2r …(5)

 

計算

式(2) 表面１部分の面積（輪っかの面積）s=2\pi RL

式(3) R\times L= ①\times②

式(4) ②=r

 

よって円の表面積は，

S=2\pi r\times①1+2\pi r\times①2+…+2\pi r\times①7

　=2\pi r(①1+①2+…+①7)

式(5)より，①の総和=2r

よって，

　=2\pi r\times 2r

　=4\pi r^2

 

\therefore S=4\pi r^2

 

パップスギュルダンの定理

：ある図形が回転してできる回転体の体積を考える。

　図形の面積をSとすると次の定理が成り立つ。

 

回転体の体積V=S\times（重心の移動距離） 

 

最後に

全記事をまとめてあります．

ぜひ下のリンクから確認してください．

uchii-memo.hatenablog.com