素数の旅
はじめに
全記事をまとめてあります.
ぜひ下のリンクから確認してください.
素数
1と自分自身以外に正の約数を持たない数(1を除く).
(例) 2, 3, 5, 7, 11, 13,…
素数は無限に存在することが知られています.
また素数の規則性はいまだ見つかっていません.
そんな謎多き素数の規則性を見つけようと,数々の数学者が挑戦してきました.
その中でも,数学の巨匠ガウスとその孫弟子であったリーマンの2人の数学者の奮闘に焦点を当てて紹介します.
ガウス
ガウスとは,1700年代に活躍した数学者のこと.
(ヨハン・カール・フリードリヒ・ガウス)
ガウスは「素数」に対して,「素数階段」を作って規則性を見出そうとしました.
ガウスの素数階段
素数のときだけ1段あがる階段

実際に素数階段をつくって見ました.
この図をみて当時のガウスはどのように考えたのでしょうか.
ガウスはこの図の概形を関数で近似しようと考えました.
ガウスの素数定理
素数階段とこの関数を重ねて表示してみます.

少しずれてますね.
しかし素数の表現に対数を使おうとした発想がとてもおもしろいと思います.
それを予想としてメモに残しました.
ガウスの予想
任意の自然数と
以下の素数の個数
についてある関係性がありそうと考えました.
ガウスの予想
(
以下の素数の個数)
ここでもまた素数の表現に対数を用いています.
実際に予想が当たっているのか確認してみます.
ガウスの予想と真値の誤差を検証しました.

の値を大きくすれば,徐々に誤差が小さくなっていることが分かる.
このままの値を大きくすれば,もっと誤差が小さくなると考えられそうです.
→ガウスの予想は当たっていそう?
素数と対数に関係がありそうと考えましたが,結論には到達しませんでした.
この後,ガウスの素数研究を孫弟子であるリーマンが継ぎました.
リーマンの素数研究について紹介します.
ベルンハルト・リーマン
ガウスの孫弟子に当たる人物です.
ガウスの素数階段を継いで「素数の規則性」について研究を進めました.
リーマンの素数階段
古い「ガウス式」の素数階段に変わり,新しい「リーマン式」の素数階段が開発されました.
リーマンの素数階段
素数のべき乗
のとき
段あがる
(例) のとき(
なので)
段上がる
のとき(
なので)
段上がる
のとき(
なので)
段上がる
実際にリーマン式の素数階段を作りました.

ガウス式とリーマン式と並べて比較してみます.
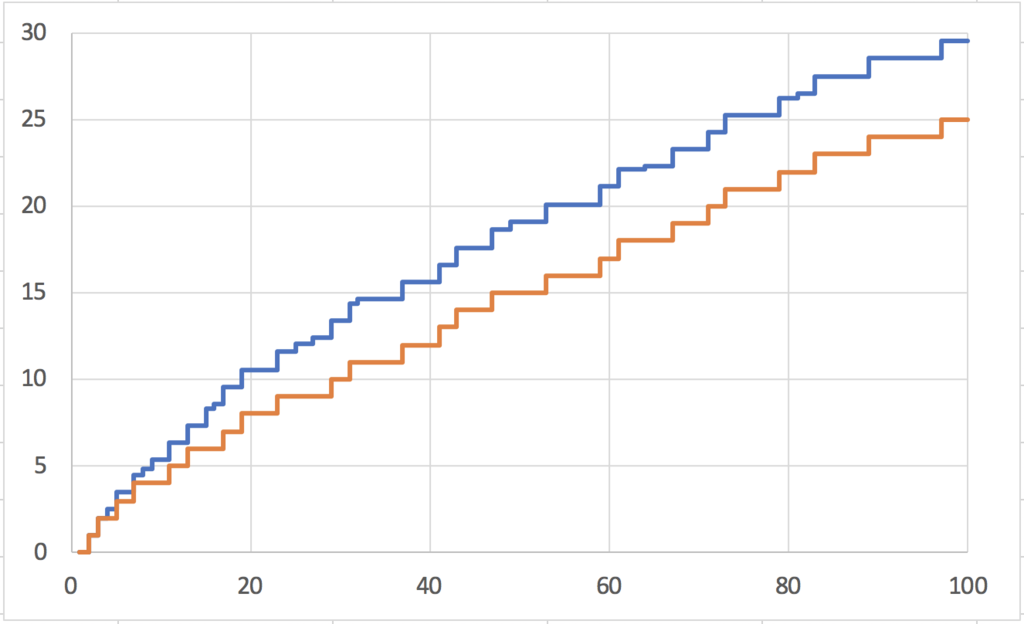
(赤=ガウス式,青=リーマン式)
ガウス式に比べて,リーマン式のほうが段数が多く細かいことが分かります.
どうして新しく素数階段を作ったのでしょうか.
リーマン式にすることでどのようなメリットがあるのでしょうか.
ずばり,素数定理との相性にメリットがありました.
リーマンの素数階段と素数定理
ガウス式の素数階段では,素数定理のグラフと近似できていませんでした.
では,リーマン式ではどうでしょうか.

無事に素数階段を関数で近似することができました.
ここからようやく「素数の規則性」について考察がスタートしました.
素数研究のその後
素数はいまだそれっぽい規則性は見つかっていません.
素数階段を用いた規則性の探索も大きな壁にぶちあったようで,結局は規則性にたどり着くに至らなかったらしいです.
しかし様々な数学者が,様々な発想で「素数の規則性」に挑む姿はとてもおもしろいので今回記事にしました.どうでしたか?
最後に
全記事をまとめてあります.
ぜひ下のリンクから確認してください.